帰無仮説

差がないと仮定するのが帰無仮説

坂巻は帰無仮説を「誤っていることを示したい「正しい」と想定したモデル」とし，対立仮説を「正しいことを示したい「正しい」と想定したモデルと定義している¹⁾．石居は 検定を行うには棄却検定法とよぼれる方法が魅入られ，そのための統計学上の仮説がたてられる．その仮説が帰無仮説であり，この帰無仮説と反対の仮説が対立仮説である としている²⁾．帰無仮説は対照と処理では「差がない」として仮説検定が行われる．すべての場合において，差があることを証明することは不可能なので，差がないことを証明する方法がとられている³⁾

¹⁾ 坂巻顕太郎・篠崎智大　2023　生物統計学の道標　一般財団法人 厚生労働統計協会  P 77

²⁾ 石居　進　1975　生物統計学入門　培風館  P 67

³⁾ 川瀬雅也・松田史生　2021  生命科学・生物工学のための間違いから学ぶ実践統計解析  p 32 – 33　

仮説検定における帰無仮説一覧

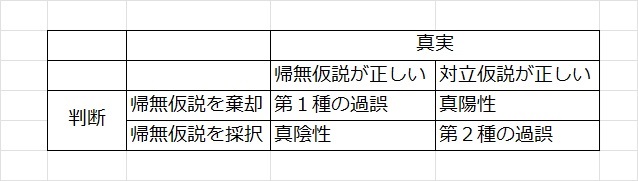
図 1 が示すように帰無仮説は「差がない」とする仮説であると考えても大きな間違いはないと考える．これは上述の説明の「すべての場合において，差があることを証明することは不可能なので，差がないことを証明する方法がとられている」ことから理解できる．

第１種の過誤 および 第２種の過誤

図 2 は 坂巻の統計的花成つ検定の判断の図を簡略化したものである⁴⁾．第１種の過誤とは，帰無仮説が正しいのに帰無仮説を棄却してしまうミスのことである．第２種の過誤とは，帰無仮説が間違っているのに帰無仮説を採択してしまうミスのことである．統計的仮説検定では，第１種の過誤および第２種の過誤が起きないように検定の性能を担保している⁴⁾．

⁴⁾ 坂巻顕太郎・篠崎智大　2023　生物統計学の道標　一般財団法人 厚生労働統計協会  P 79

片側検定と両側検定

処理によって対象とする特性が影響を受けるとき，たとえば測定が数値であるならば，数値が増加する場合と数値が減少する場合がある．植物に矮化剤を処理すれば草高は低くなり，ジベレリンを処理すれば草高は高くなる．処理の効果は特性を数値的に大きくするのか，小さくするのかは実験をするまではわからない．このため，数値が大きくなる場合とちいさくなる場合を仮定して検定することを両側検定といい，大きくなる場合だけ，あるいは，小さくなる場合だけを想定して検定することを片側検定という．ふつう検定には両側検定が用いられる．

まとめ

(1) 帰無仮説を「誤っていることを示したい「正しい」と想定したモデル」とし，対立仮説を「正しいことを示したい「正しい」と想定したモデルと定義できる．

(2) 帰無仮説は「差がない」とする仮説であると考えても大きな間違いはないと考える．

(3) 第１種の過誤とは，帰無仮説が正しいのに帰無仮説を棄却してしまうミスのことである．第２種の過誤とは，帰無仮説が間違っているのに帰無仮説を採択してしまうミスのことである．

(4) 統計的仮説検定では，第１種の過誤および第２種の過誤が起きないように検定の性能を担保している．

(5) 数値が大きくなる場合とちいさくなる場合を仮定して検定することを両側検定といい，大きくなる場合だけ，あるいは，小さくなる場合だけを想定して検定することを片側検定という．ふつう検定には両側検定が用いられる．