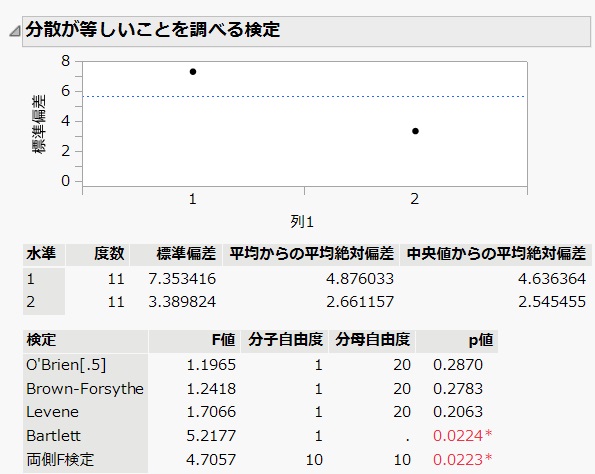
Leven 検定および F 検定
対照と処理のように,集団 A と 集団 B が同一集団に属するかどうかの検定,つまり,対照 と処理が異なる集団であるかどうかの検定について解説する.対照 と処理が異なる集団であるならば,この処理によって何らかの効果があったと考えるということになる.2 つの集団が同一集団の属するということは,分散と平均値が等しいということである 1) .したがって,第 1 に 2 つの集団の分散が等しいかどうかを検定し,第 2 に 2 つの集団の平均値が等しいかどうかの検定をする必要がある 2) .なお,2 つの集団の平均値が等しいかどうかの検定としては,スチューデントの t 検定を解説する.
1), 2) 石井 進 1975 生物統計学入門 培風館 東京 p.161
Leven 検定および F 検定は,2 つの集団の分散が等しいかどうかを調べる検定である. これまで多くの生物統計学の書籍では,2 つの集団の分散が等しいかどうかを調べる検定として F 検定を解説している 3),4),5).一方,ビジネス・アナリティクスのソフトウェアとサービスの会社 SAS による統計解析ソフト JMP には Leven 検定が実装されおり( F 検定も実装されている),この 2 つの検定のうちいずれかを使うことになる.
3) 石井 進 1975 生物統計学入門 培風館 東京 p.161
4) Robert R. Sokal・F. James Rohlf 藤井宏一 訳 生物統計学 1983 共立出版 東京 p.162
5) 東京大学教養部統計学教室 編 1991 統計学入門 東京大学出版会 東京 p.245
安全性評価研究会の Web サイトにおいて薬学博士 松本一彦 氏は,F 検定と比べると,Leven 検定のほうが 外れ値の影響を受けにくいことを示している 6).Leven 検定では,偏差の絶対値をもとに検定するが,F 検定では偏差の 2 乗 をもとにして検定するので,外れ値が存在した場合は,偏差を 2 乗する F 検定のほうが数値が大きくなるため影響を受けやすくなるのである.このブログでは,ケースバイケースで Leven 検定あるいは F 検定を使うことにする.
6) https://tanigaku.jp/wp/?p=2463
F 検定の帰無仮説は 2 つの集団の分散は等しい である.Leven 検定の帰無仮説は すべての集団の分散は正しい であって,Leven 検定では 2 つ以上の集団についての等分散性を検定することができる.
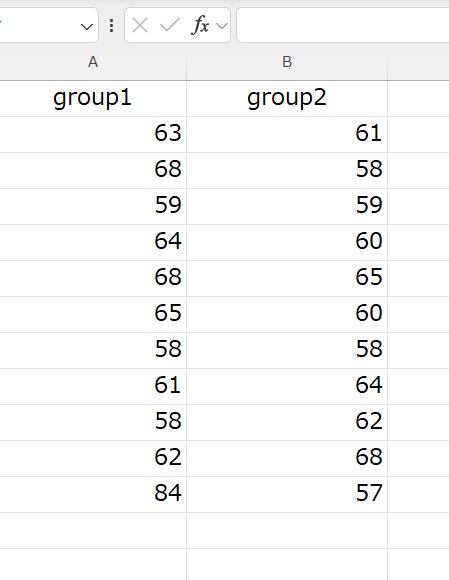
group1 および group2 の分散が同じ(等分散)であるかを JMP で調べた結果を下に示した.