サンプルサイズとサンプル数

サンプルサイズとサンプル数はまったく異なる概念である．これことを認識しないと統計解析の結果を正しく理解することはできない．

サンプルサイズ

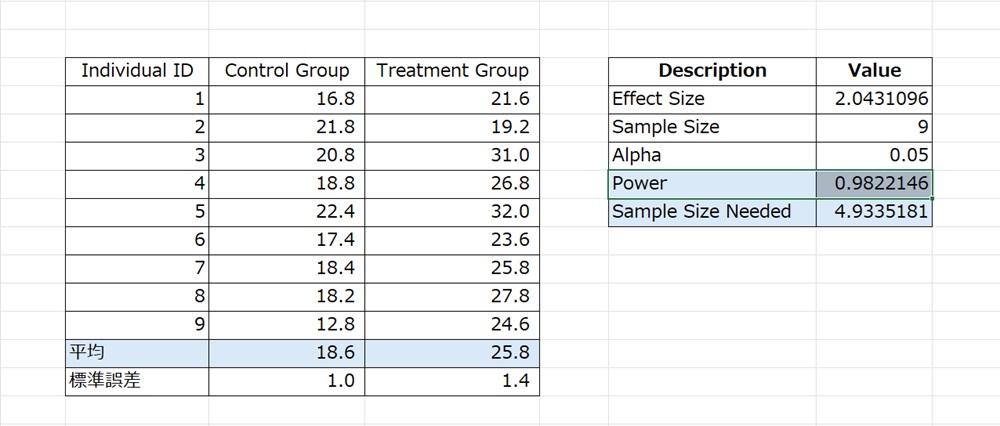
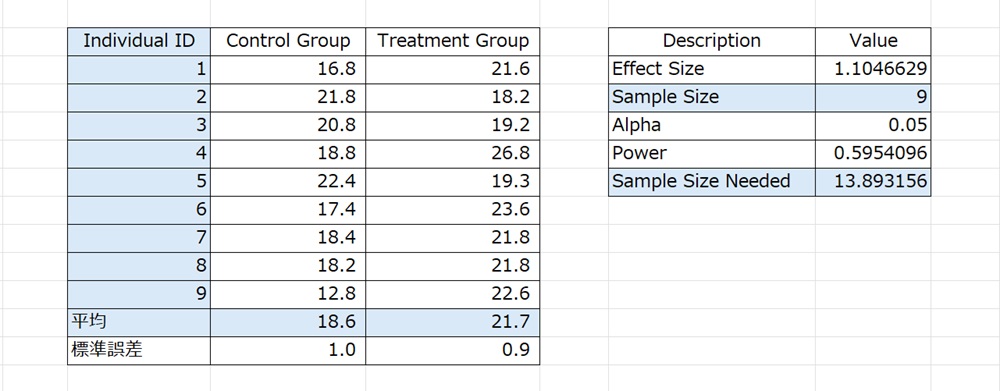
右の表の Sample Size (サンプルサイズ)は 9 になっている．左の表のIndividual ID (個体番号) は 9 であることから，サンプル数は 9 であることが理解できる．右の表の Sample Size Needed(必要なサンプルサイズ) は 13.89･･･であるから，サンプルサイズは 9 になり，サンプルサイズはすくなくて 14 必要であることが示されている．つまり，サンプル数は統計解析に使用したサンプル数を表し，サンプルサイズは 正確に統計解析するために必要なサンプル数のサイズを示していることになる¹⁾．

サンプル数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　統計解析に使ったサンプルの数を示す

サンプルサイズ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　正しく統計解析するために必要なサンプル数がどのくらいサイズであるかを示す　　　

¹⁾ 池田郁男 改訂増補版：統計検定を理解せずに使っている人のために Ⅰ　2019 化学と生物 57(8) P.201 

統計解析に必要なサンプルサイズ

下の２つの表は説明に使った表よりも処理の平均が大きくなるように作成している．平均が 25.8 のときは，必要とするサンプルサイズは 4.933･･･であり，平均が 32.5 のこときの 必要とするサンプルうサイズは 2.850･･･と小さくなっている．この表からわかることは，対照と処理の平均の差が大きいと統計処理を正しくおこなうための サンプルサイズはちいさくなっていくということである．つまり，対照と処理の平均に差があるほどサンプル数はすくなくてもよいことになる．

このブログで扱うような統計解析では，サンプルサイズは 5 ～ 30 くらいとされている²⁾．このくらいのサンプルサイズでの統計解析する統計学は小標本統計と呼称されている³⁾．

²⁾ 石居　進 生物統計学入門 1975 培風館 P.46,47,53

²⁾ 清水信博 もう悩まない！論文が書ける統計 2004 オーエムエス出版 P.59

これからながながと解説していく統計的有意性検定（NHST：Null Hypothesis Significance Testing）は、長い間標準的な方法であったが，統計的有意性検定の結果だけで対象とする現象・特性を考察することは否定されつつある．統計的有意性検定のサンプルサイズは上述のように 5 ～ 30 くらいである．サンプル数をこのくらいの範囲におさめるためには，①分析・観察の精度を上げること および ② 対象にする集団の特性を代表する個体を抽出すること が必要になる．

まとめ

(1) サンプルサイズとは 正確に統計解析するために必要なサンプル数がどのくらいサイズを示す数値である．

(2) 対照と処理の平均に差があるほどサンプル数はすくなくてもよい．