確率分布はいくつかの種類があり,それぞれ異なる特性を持っているので,その特性に適した統計解析やモデリングに使用されている.研究やデータ解析の目的に応じて、適切な確率分布を選択しなければ適切な統計解析はできない.
確率変数および確率分布
確率変数および確率分布について説明する.ダーツの矢を高さ 1 m から落とし,下の平面に定めた1点 および 落としたダールの矢の距離(データとする) を測定する実験 を考えることにする.定めた1点とダーツの矢の距離は,ダーツの矢を離すときの,指の力を緩める程度,実験場の風速,矢がおちる間に通過する空気の状態など に影響されて,連続的な値(データ)を示すことになる.ダーツの矢が落ちた点 と 定めた1点との距離は、理論上、無限に小さな値として計測できるため、得られるデータは連続変数とみなすことができる.
ダーツの矢を高さ1mから落とすこの実験では、矢が落ちる場所はランダムであり、定めた1点からの距離は ランダムに変動する ので,ある実験の結果として得られる数値(データ)を表す変数,すなわち確率変数とみなすことができる.確率変数は連続的な値を取り,ある範囲の中で特定の確率密度関数 (probability density function, PDF) に従う.この場合、確率密度関数は距離に応じて異なる確率を割り当てる関数になる.確率密度関数が特定の点で取る値を確率密度といい,このような関数による分布を確率分布という.
さいころを振ってでたさいの目をデータとする実験を考えることにする.さいの目が 4 である確率を考えると,6 通りのさいの目がでる場合があり,4の目がでる確率は,1 ÷ 6 ≒ 0.167 となる.この場合は得られるさいの目は,1 ~ 6 までの 6 であるため,データとして得られるさいの目は 6 通りになり,連続的な値ではなく,離散した値になる.さいころの目はランダムにでるので,ある実験の結果として得られる数値(データ)を表す変数,すなわち確率変数とみなすことができる.この場合、確率密度関数はサイコロの目の値に応じて異なる確率を割り当てる関数になる.
ダーツの矢の実験のように連続した値をとる確率分布を連続型確率分布といい,さいころの実験のように分散した値をとる確率分布を離散型確率分布という.
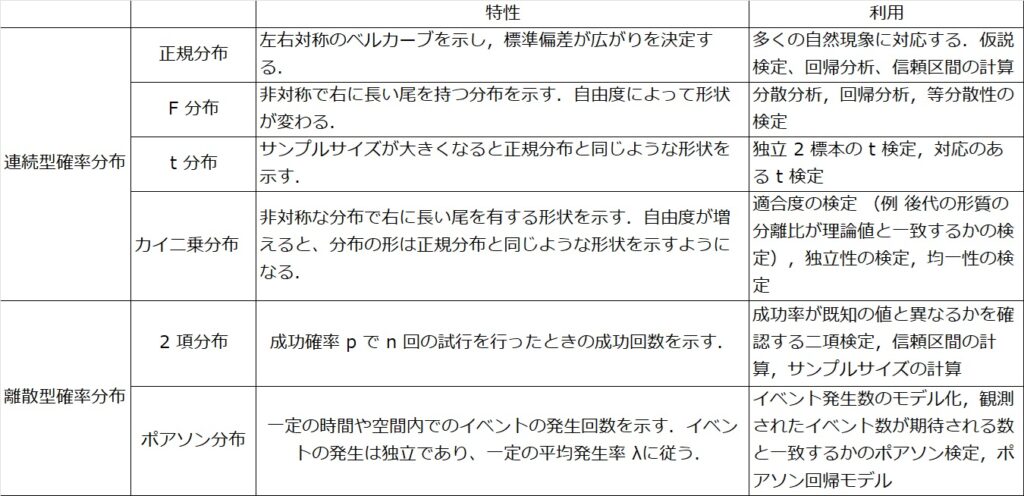
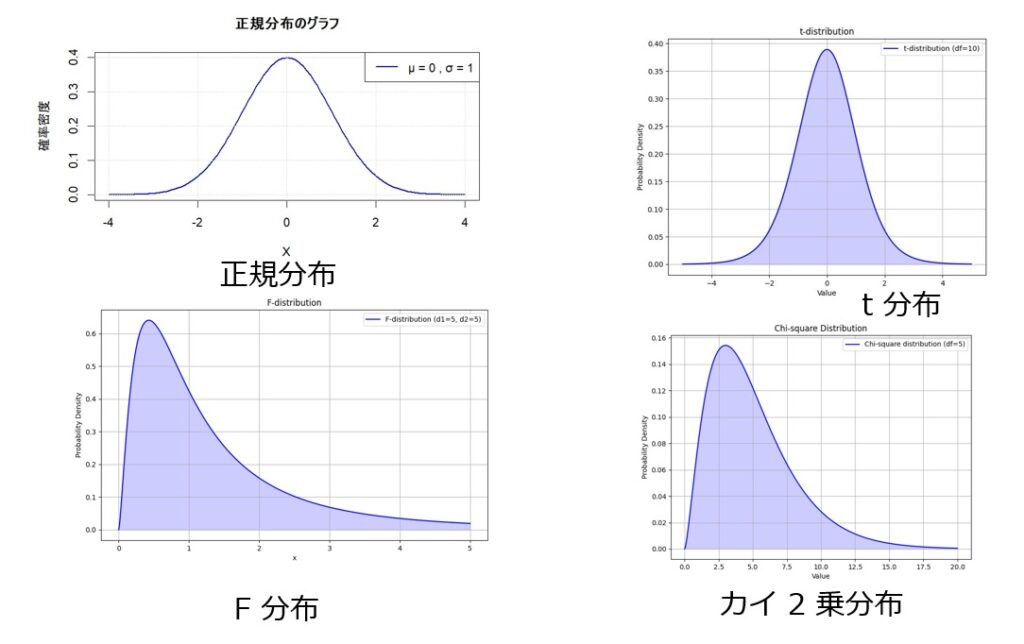
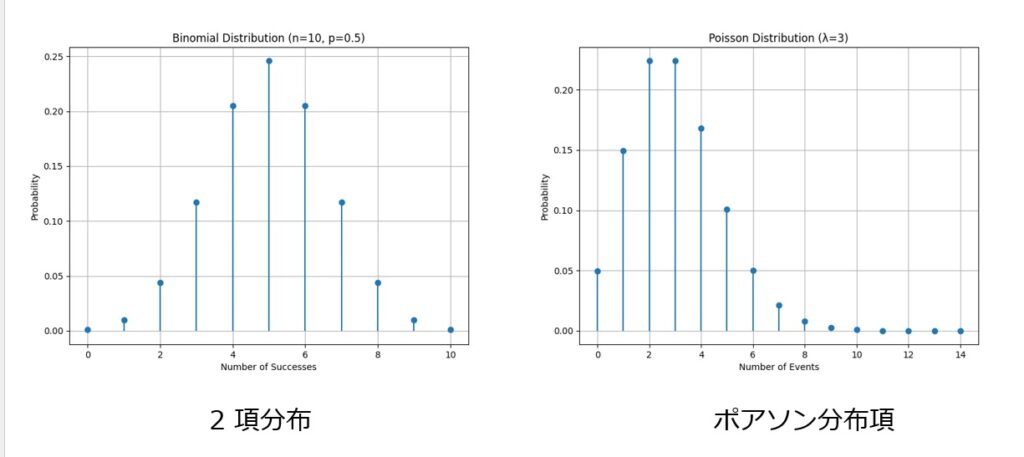
連続型確率分布および離散型確率分布が統計学的に意味を持つのは,これらは,実験あるいは観察によって得られるデータの分布のモデルになるからである.以下に確率分布の種類を示し,その特性および統計解析における利用を示す.